
Here we will learn about scale maths, including scale diagrams and scale drawing, scale factors and real life applications.
There are also scale maths worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
Scale maths is a way of enlarging an object.
If we have two shapes that are similar, one will be a scale diagram of the other.
We can calculate the scale factors for length, area and volume.
Let’s look at this example,
The length scale factor can be calculated by comparing two lengths.
We can compare the length of A with the length of B.
This gives the ratio 3:6 which simplifies to 1:2.
The length scale factor from A to B is \bf .
The area scale factor can be calculated by comparing two areas.
We can compare the area of A with the area of B.
Area A = 3cm \times 3cm = 9cm^
Area B = 6cm \times 6cm = 36cm^
This gives the ratio 9:36 which simplifies to 1:4.
The area scale factor from A to B is \bf .
The volume scale factor can be calculated by comparing two volumes.
Volume A = 3cm \times 3cm \times 3cm = 27cm^
Volume B = 6cm \times 6cm \times 6cm = 216cm^
This gives the ratio 27:216 which simplifies to 1:8.
The volume scale factor from A to B is \bf .
We can square the length scale factor to calculate the area scale factor.
We can cube the length scale factor to calculate the volume scale factor.
In the above example,
Scale factor for length = \bf
Scale factor for area = 2^2 = \bf
Scale factor for volume = 2^3 = \bf
Step-by-step guide: Scale diagram

Scale maths is used for real world scale drawings as it is much easier to create a scale drawing of an object, than to draw the object using actual distances.
The ratio usually takes the form 1:n of the model/plan to the actual distance.
Below is a scale diagram of a floor plan of a house where 1 square is equal to 2 metres.
Writing this as a ratio we get \bf square: \bf
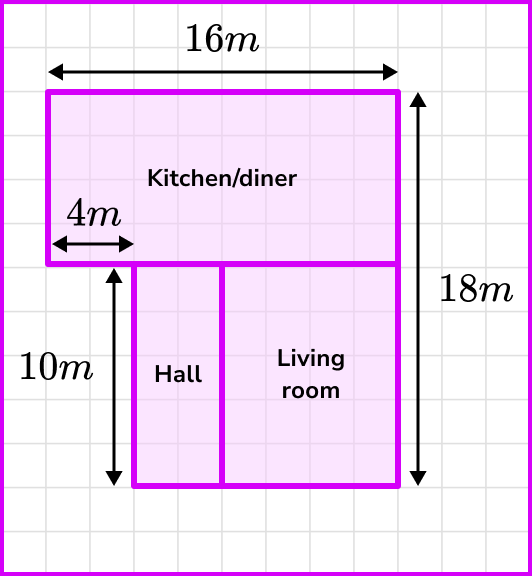
From this diagram, we can calculate the width of the living room by counting squares.
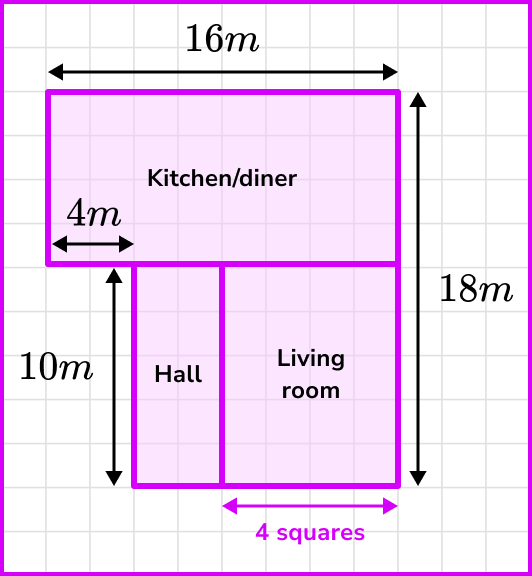
As the living room is 4 squares wide and we have the ratio 1 square: 2m, multiplying the number of squares by 2 we get the actual width of the living room.
4 \times 2=8m so the living room is 8m wide.
Step-by-step guide: Scale drawing
In order to calculate the actual / real life distance from a scale:
In order to calculate the model length from a scale:
In order to calculate a ratio from a scale diagram:




Get your free scale maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.


Get your free scale maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.
A map has a scale of 1cm:5km. Find the actual distance represented by 3cm on the map.
2 Multiply \bf by the length given from the model.
3 Write the units.
The construction plans for a structure has the scale 2cm:3m. What is the actual distance of 62cm on the plan?
State the scale of the enlargement as a ratio in the form \bf
We have the ratio 2cm:3m which we can express as the ratio 1cm:1.5m or in centimetres, 1cm:150cm.
Multiply \bf by the length given from the model.
62 \times 150=9300cmWrite the units.
9300cm \text < or >93mA map of the UK is drawn using the scale 30cm:1500km. Calculate how far 480km would be on the map.
Divide the real life distance by the map scale ratio.
Before we do this, let’s convert the ratio to the form 1 \ cm:n \ km by dividing both sides of the ratio by 30.
Now we can calculate the length on the map.
Write the units.
A plan of a kitchen uses the scale 5cm:20cm. Calculate the distance on the plan for the actual distance of 8.7m.
Divide the real life distance by the map scale ratio.
Before we do this, let’s convert the ratio to the form 1 \ cm:n \ cm by dividing both sides of the ratio by 5.
We also can convert 8.7m to centimetres by multiplying it by 100 .
Write the units.
A kite has a vertical height of 28cm and a width of 12cm. The scale diagram of the same kite has a width of 8cm.
What is the ratio of the real kite to the scale diagram? Write your answer in its simplest form.
Identify two lines that are mathematically similar.
Here we have the two widths of the kite with the lengths 12cm and 8cm.
Express the lengths as a ratio \bf
The ratio is of the form actual : scale diagram so we have the ratio
Simplify the ratio.
Writing the ratio in the simplest form (divide throughout by 4 ) we have
The circumference of Jupiter is 439,624 \ km. A scale model of the planet has a diameter of 11.2 \ cm. Calculate the ratio of the scale diagram to the real planet Jupiter.
Give your answer if the form a \ cm:b \ km. Write a and b correct to 2 significant figures.
Identify two lines that are mathematically similar.
The circumference of a circle = \pi \times diameter and so the circumference of the scale diagram of Jupiter is
C= \pi \times 11.2=35.185. cm.
We can now use the two circumferences 35.185. cm and 439624 \ km.
Express the lengths as a ratio \bf
The ratio is of the form scale diagram : actual so we have the ratio
35.185. cm:439624 \ km .
Simplify the ratio.
This ratio cannot be simplified but we could round the values to make them easier to read. Rounding the ratio, we get
35 \ cm:440 \ 000 \ km .
A common error is to multiply the real life distance by the ratio scale instead of dividing, giving an incorrect distance on the plan.
A common misconception is to divide the distance on the model / plan / map by the ratio scale resulting in an incorrect real life distance.
Stating the ratio in the incorrect order will mean that the scale diagram is much larger / smaller than expected.
For example, a ratio represents the scale diagram to the real life distance. The ratio 1:2 means that the real life distance is twice the length of the scale diagram. The ratio 2:1 on the other hand means that the real life distance is half of the scale diagram.
If given the ratio 2 \ cm:5 \ km, it is easier to calculate when the ratio is in the form 1:n and so we must find an equivalent ratio before using the scale.
Here the ratio would be 1 \ cm:2.5 \ km so 1 \ cm on the map would be equal to 2.5 \ km in real life
A common misconception is to mix up the units for the model with the units for the real life distance.
For example, if we were calculating the distance of 10 \ cm on a map with the scale ratio of 1 \ cm:5 \ km, \ 10 \times 5=50 \ cm could be incorrectly stated. Whereas the correct solution would be 10 \times 5=50 \ km.
Sometimes the units need to be converted, so it is important to be able to confidently convert between different metric units.
For example, the map scale is given as 1:25 \ 000 which means that 1 \ cm on the map is equivalent to 25 \ 000 \ cm in real life. If the answer need to be be written in kilometres, the real life value in centimetres must be divided by 100 \ 000 to get the same measurement in kilometres. 1:25 \ 000=1 \ cm:0.25 \ km.
1. A map has a scale 1:125 \ 000. The distance between two points on the map is 3.8 \ cm. What is the real distance in kilometres?